Compilers for Sound Floating-Point
Explanation
Floating-point data types are a natural choice for software developers when implementing numerical computations. They are widely used in computer science and engineering, including in cyber-physical systems that interact with the physical world. Unfortunately, floating-point numbers do not exactly represent real values and thus can suffer from roundoff errors. Further, their non-intuitive nature can make it hard to predict when and how these errors accumulate to the extent that they invalidate the final result. Thus, it is important to provide guarantees (i.e, sound floating-point arithmetic) and do so fast for any given input.
We introduce IGen, a source-to-source compiler that translates a numerical program performing floating-point computations to an equivalent sound numerical program using interval arithmetic (IA) or affine arithmetic (AA). By sound we mean that the resulting intervals are guaranteed to contain the result of the original program if it were performed using real arithmetic.
Overview
The picture below provides an overview of IGen’s internal structure. The input is a C function, possibly using SIMD intrinsics, performing floating-point computations and a target precision for the interval endpoints or affine error symbols. This target precision can be either single or double precision (the default) or the higher double-double precision. The output is an equivalent C function performing the same computation soundly using IA or AA, optionally optimized with SIMD intrinsics.
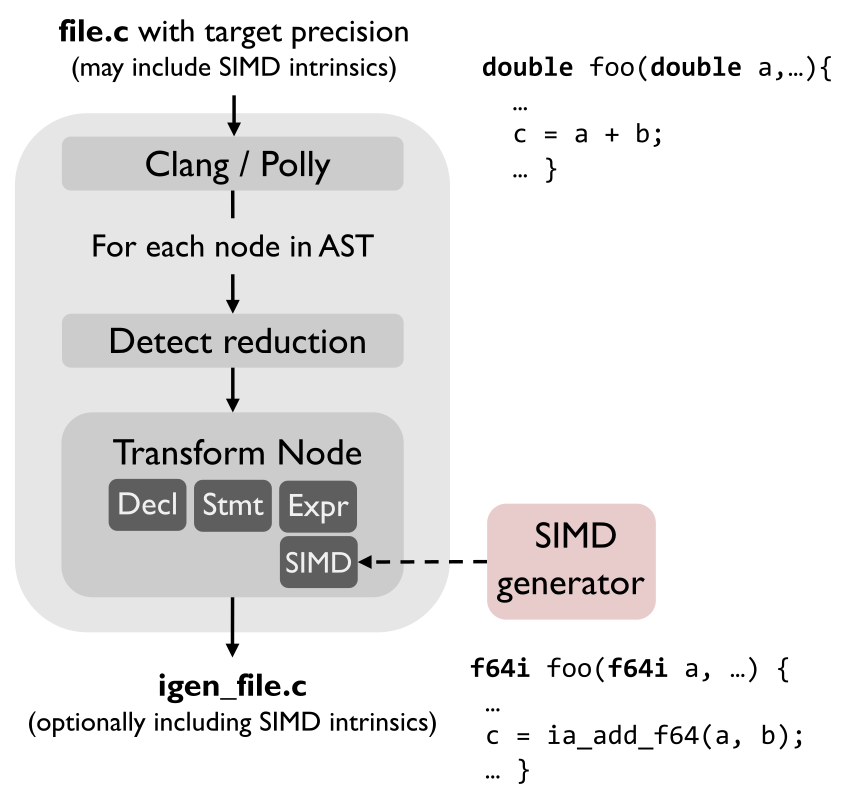
IGen uses the Clang LibTooling library to construct the abstract syntax tree (AST) of the computation. The AST is then traversed and, for each node, an equivalent set of interval operations is generated, possibly in increased precision. The support of SIMD intrinsics in the input function is handled by a generator that automatically produces the interval implementation of (a large subset of) SIMD intrinsics from its XML specification.
Improving accuracy. When generating IA code, IGen uses Polly and a transformation technique to improve the accuracy of the common reduction pattern in linear-algebra-like computations. In AA mode, we implemented a preprocessing step that analyses the DAG of the computation and identifies affine variables that are likely to improve accuracy.
Evaluation
We evaluated IGen on an Intel Xeon E-2176M CPU (Coffee Lake microarchitecture) running at 2.7 GHz, under Ubuntu 18.04 with Linux kernel v4.15. Turbo Boost is disabled. All tests are compiled using gcc 7.5 with flags -O3 -march=host. To evaluate performance, we use RDTSC to measure the cycle count for each test, performing 30 repetitions with warm cache, and using the median as a result. The accuracy of an interval is determined as the number of most-significant bits shared by the mantissas of the endpoints assuming same exponent. (An affine result is first transformed to an interval to compute its accuracy.)
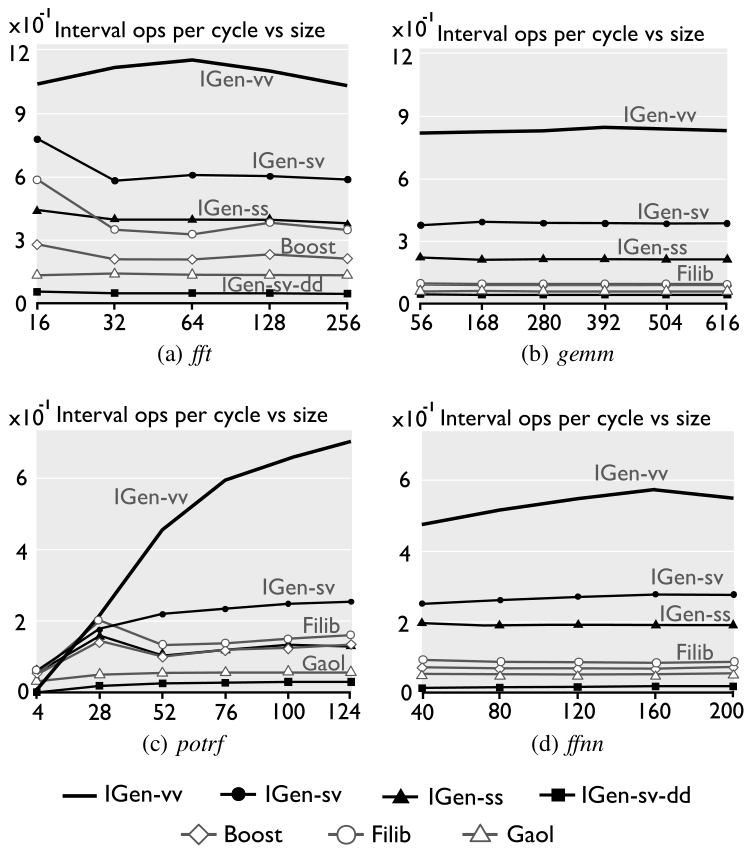
For each benchmark, IGen generates interval code with the following configurations:
- IGen-ss: scalar code generated from scalar input code.
- IGen-sv: vectorized code (SSE) from scalar input code.
- IGen-vv: vectorized code (AVX) from vectorized code.
- IGen-sv-dd: as IGen-sv but with double-double precision output.
Performance. The figures below show the performance (in interval operations per cycle) of IGen and other interval libraries for a set of benchmarks. The problem size is on the x-axis and the interval operations (iops) per cycle on the y-axis. Here, an interval multiplication and an addition count as one operation each.
Runtime-accuracy tradeoff of the AA configuration.
We present now the results of IGen in AA mode for benchmarks that are known to perform poorly in IA. The pareto plots below show the runtime-accuracy tradeoff of different configurations of IGen and others AA libraries. Configurations closer to the bottom-right corner are pareto optimal (i.e. they present higher accuracy and lower slowdown). The configurations generated by IGen are the following:
- f64a-dspv: AA vector code generated from scalar input code. (Red circles)
- IGen-f64: IA vectorized code from scalar input code. (White circle)
- IGen-dd: IA vectorized code with double-double precision output. (White rhomb)
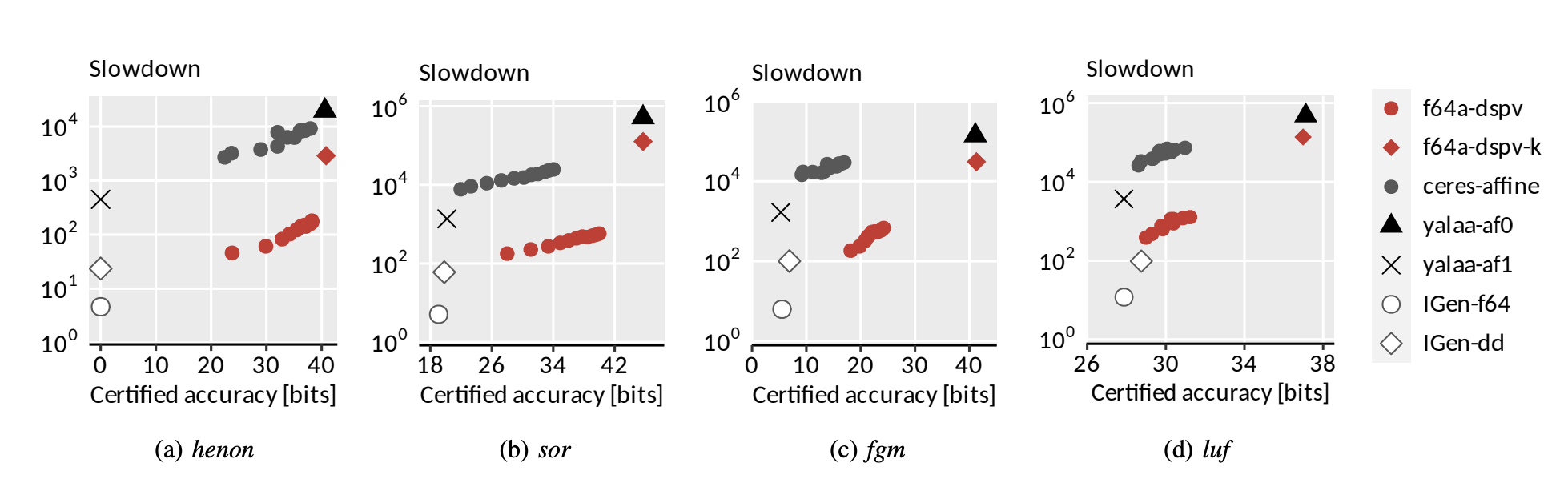
As can be seen, f64a-dspv (IGen with AA) is able to preserve a considerable higher accuracy for these benchmarks compared to IGen-f64 and IGen-dd (IGen with IA).
References
-
Joao Rivera, Franz Franchetti, Markus Püschel
An Interval Compiler for Sound Floating-Point Computations
in Proc. Code Generation and Optimization (CGO), pp. 52-64, 2021 -
Joao Rivera, Franz Franchetti, Markus Püschel
A Compiler for Sound Floating-Point Computations using Affine Arithmetic
in Proc. Code Generation and Optimization (CGO), pp. 66-78, 2022

