Clover: 4-bit Quantized Linear Algebra

Clover is a new library for the efficient computation on low-precision data, providing mathematical routines required by fundamental methods in optimization and sparse recovery. Our library faithfully implements variants of stochastic quantization and supports 4-bit quantized and 8-bit quantized data formats and demonstrate that 4-bit can be implemented efficiently using Intel AVX2 despite the lack of native support for this data format.

Clover also supports 16-bit half precision and 32-bit single precision IEEE-754 formats that are natively supported by Intel processors. Experimental results with dot product, matrix-vector multiplication, gradient descent (GD), and iterative hard thresholding (IHT) illustrate the attainable speedups, in many cases close to linear in the reduction of precision because of reduced data movement.

This library is implemented in collaboration with Tyler Michael Smith as a research project at Department of Computer Science at ETH Zurich, supervised by Dan Alistarh and Markus Püschel. Experimental results of this work are published at SIPS 2018 and are accessible in the pre-print version here.

Clover Data Structure

Quantization is a lossy compression technique that maps continuous values to a finite set of fixed bit-width numbers. For a given vector $v$ of size $n$ and precision of $b$ bits, we first derive a factor $s_v$ that scales the vector elements $v_i$ into the representable range:

$$ s_v = \frac{2^{b-1} - 1}{\max_{i \in [1, n]} |v_i|}. $$

The scaled $v_i$ are then quantized stochastically:

$$ v_i \rightarrow \left\lfloor v_i \cdot s_v + \mu \right\rfloor $$

where $\mu$ is drawn uniformly from the interval $(0,1)$. With this, a quantized array consists of one scaling factor and an array of quantized $b$-bit values.

Functionality for quantized 4-bit linear algebra operations is provided by the CloverVector4 and CloverMatrix4 containers. CloverVector4 contains a vector represented in a quantized 4-bit format. The values and the scaling factors are stored in separate contiguous blocks of memory, such that sub-vectors of length 64 share the same scale.

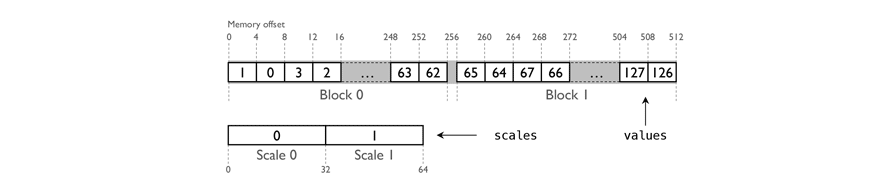
An illustration of the memory layout of a CloverVector4 container is shown above. Each value in the vector is stored as a two’s complement in a 4-bit nibble. The x86 architecture uses byte addressing, so we address each the nibbles in software. We accomplish this explicitly in the application logic, storing two consecutive nibbles in a byte. As a result, the values in a CloverVector4 of length n are represented as an array of n/2 bytes. CloverVector8 shares the same design principles. CloverVector16 and CloverVector32 containers do not have scales, and the data layout is not organized into blocks.

A simplified C++ representation of the CloverVector4 container is shown below:

class CloverVector4 {
  protected:
    uint64_t length;
    int8_t * values;
    float  * scales;
}

The 4-bit values stored in the values array are in the range of $\left[-7, 7 \right]$, therefore each element at position pos is obtained by multiplying the value with the corresponding scale, and dividing the result by 7.0f. Therefore get routine will have the following form:

inline float get(uint64_t pos) const
{
    const uint64_t idx   = pos >> 1;
    const uint64_t block = pos >> 6;

    const float scale = scales[block] / 7.0f;
    const int8_t qu_p = values[idx];

    return scale * (float) _mm_srai_epi8_ss(qu_p << (pos % 2) * 4, 4);
}

where _mm_srai_epi8_ss performs right bit shifts, extending in sign bits, and operates on 8-bit integers.

Fast Packing and Unpacking of 4-bit values

The x86 architecture does not support 4-bit integer arithmetic. Thus we unpack the values, representing them as larger (i.e., 8, 16 or 32-bit) integers for computation. Then, for efficient storage and data movement, we pack these larger integers, representing them as 4-bit integers stored within a larger entity.

The goal of unpacking from a 32-bit integer (right part of figure below) is as follows: We start with a 32-bit entity that stores multiple nibbles inside of it. We wish to extract a single 4-bit nibble and represent it as a 32-bit integer. This can be done with two bit shifts:

• (1) a logical left shift is used to shift the nibble so that it occupies the highest-order 4-bits of the 32-bit entity.
  
• (2) an arithmetic right shift is used to shift the nibble to the lowest order 4-bits of the 32-bit entity.

The arithmetic right shift has sign extension, filling the high-order 28 bits with the sign bit of the nibble. yielding a 32-bit integer with the same value as the two’s complement 4-bit value.

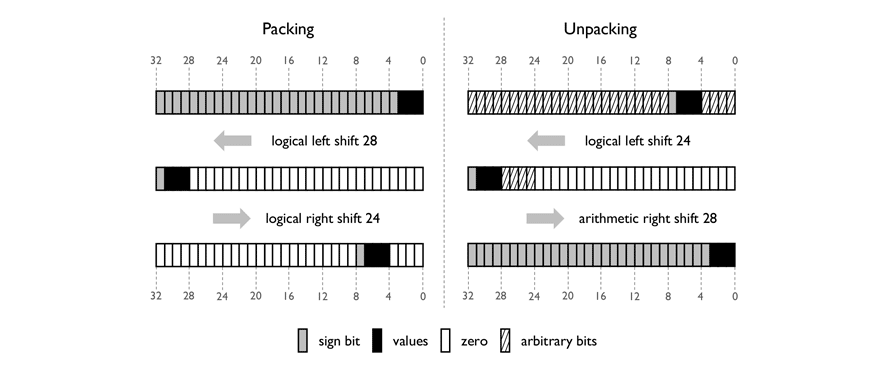
The goal of packing (left part of figure above) is to revert the unpacking operation. Two bit shifts can be used to place the lowest order 4 bits of a 32-bit integer anywhere within a 32-bit entity.

(1) a logical left shift is used to shift the nibble so that it occupies the highest-order 4-bits of the 32-bit entity. (2) a logical right shift is used to shift the nibble to somewhere within the 32-bit entity.

The first sets the bits lower-ordered than the nibble to zero, and the second sets the bits higher-ordered than the nibble to zero. A bitwise OR operation can then be used to store up to eight nibbles in the 32-bit entity.

Dot Product in Clover

Taking in consideration the fast packing and unpacking, as well as the structure of the Clover containers, let’s illustrate how we can write a fast dot product routine using AVX2. Let’s assume that we like to perform dot product on two vectors U and V.

We denote the values of the U vector with the following variables:

const int8_t * u = ... ; // the array of 4-bit quantized values
const float * su = ... ; // the array of 32-bit floating point scales

And the vector V with:

const int8_t * v = ... ; // the array of 4-bit quantized values
const float * sv = ... ; // the array of 32-bit floating point scales

Now, let’s setup the constants and initialize the accumulator for the result variable:

// we initialize the accumulator to 0
__m256 dot_product_acc  = _mm256_setzero_ps();

// we setup the constants that are going to be used later
const __m256  clover_mm256_rcp_49_ps        = _mm256_set1_ps(1.0f / 49.0f);
const __m256i clover_mm256_1st_bit_set_epi8 = _mm256_set1_epi8  (-16);
const __m256i clover_mm256_1_epi16          = _mm256_set1_epi16(1);

Since values are stored in blocks of 64 elements, we will traverse each block using iterator i, loading quantized values of 4-bits and their corresponding block scales:

offset = i * 64 / 2;

// Load two quantized values
const __m256i qu = _mm256_loadu_si256( (__m256i *) (u + offset) );
const __m256i qv = _mm256_loadu_si256( (__m256i *) (v + offset) );

// Load the scales by boradcasting them into an AVX register
const __m256 su = _mm256_broadcast_ss(su + i);
const __m256 sv = _mm256_broadcast_ss(sv + i);

The dot product routine requires all values to be multiplied point-wise, before the result is reduced by summation. Therefore, once we have the scales, we can multiply them, while scaling each with factor of 7.0f. However, division instructions are expensive, and we can use multiplication with the reciprocal value of 49.0f (stored into clover_mm256_rcp_49_ps) instead:

const __m256 su_scaled  = _mm256_mul_ps(su, clover_mm256_rcp_49_ps);
const __m256 scaled_rcp = _mm256_mul_ps(su_scaled, sv);

The two loads from the two value arrays, result into two AVX registers that hold 64 4-bit values. As we can not operate with 4-bits natively, we will convert the 4-bit values into 8-bit integers. Assuming presence of 8-bit shifts, we can apply the fast packing/unpacking method to extract the low- and high-bits at each 8-bit chunk. However, AVX2 provides us with 16-bit shifts only.

To deal with that, we shift by 4 bits left, and then we perform bitwise AND operations, such that the low 4-bits of the 8-bit chunk are placed in the high 4-bits. To avoid dirty bits, we apply the previously defined mask in clover_mm256_1st_bit_set_epi8 to extract both the high- and low-bits of qu and qv:

const __m256i qu_lo_shift = _mm256_slli_epi16(qu, 4);
const __m256i qv_lo_shift = _mm256_slli_epi16(qv, 4);

const __m256i qu_hi = _mm256_and_si256(clover_mm256st_bit_set_epi8, qu);
const __m256i qv_hi = _mm256_and_si256(clover_mm256st_bit_set_epi8, qv);
const __m256i qu_lo = _mm256_and_si256(clover_mm256st_bit_set_epi8, qu_lo_shift);
const __m256i qv_lo = _mm256_and_si256(clover_mm256st_bit_set_epi8, qv_lo_shift);

At this point in time, we have 2 variables for qu and 2 variables for qv such that each contain 32 elements. qu_hi represents the 4 high bits, and qu_lo represents the low 4 bits. For each of these 4 variables, the extracted 4-bit values reside in the high 4-bit of the 8-bit chunk i.e. they are all multiplied by $2^4$.

Now, we would like to multiply the corresponding high/low bits of the first vector with the corresponding high/low bits of the second vector. Unfortunately AVX2 does not provide us with a vector instruction that can multiply signed 8-bit integers. Instead, it provide us with the vpmaddubsw instruction that we can use to perform this computation:

__m256i _mm256_maddubs_epi16 (__m256i a, __m256i b)

The definition of this instruction is given as: Vertically multiply each unsigned 8-bit integer from a with the corresponding signed 8-bit integer from b, producing intermediate signed 16-bit integers. Horizontally add adjacent pairs of intermediate signed 16-bit integers, and pack the saturated results in dst.

Therefore, in order to benefit from this instruction we need to make sure that left operand is unsigned and that the sign is accumulated in the right operand:

// Get absolute values of u vectors
const __m256i au_hi = _mm256_sign_epi8(qu_hi, qu_hi);
const __m256i au_lo = _mm256_sign_epi8(qu_lo, qu_lo);

// Sign the values of the v vectors
const __m256i sv_hi = _mm256_sign_epi8(qv_hi, qu_hi);
const __m256i sv_lo = _mm256_sign_epi8(qv_lo, qu_lo);

// Perform multiplication and create 16-bit values
const __m256i dot_hi = _mm256_maddubs_epi16 (au_hi, sv_hi);
const __m256i dot_lo = _mm256_maddubs_epi16 (au_lo, sv_lo);

At this point, we have computed the multiplication of corresponding elements, and we have added neighbouring elements, obtaining the result into 16-bit chunks. As the 8-bit chunks were already offsetted by factor of $2^4$, the 16-bit chunks contain values in the range of $\left[-(2^4 \cdot 7)^2 \cdot 2, (2^4 \cdot 7)^2 \cdot 2\right]$, or $\left[-25088, 25088\right]$. To continue, we shift the values right, while extending in sign bits, effectively dividing the 16-bit chunks by factor of $2^8$ (making sure that the values are in the range $\left[-98, 98\right]$):

const __m256i dot_hi_shift = _mm256_srai_epi16 (dot_hi, 8);
const __m256i dot_lo_shift = _mm256_srai_epi16 (dot_lo, 8);

Now we can simply add the two 16-bit values using 16-bit addition provided by AVX2:

const __m256i dot_16 = _mm256_add_epi16(dot_hi_shift, dot_lo_shift);

Once we a single variable that represents the dot product of the block, the last thing we need is to multiply this value with the corresponding scale. To achieve that, we need to convert the 16-bit chunk into a float. We can do this in a single instruction using vpmaddwd instruction.

__m256i _mm256_madd_epi16 (__m256i a, __m256i b)

The definition of this instruction is given with: Multiply packed signed 16-bit integers in a and b, producing intermediate signed 32-bit integers. Horizontally add adjacent pairs of intermediate 32-bit integers, and pack the results in dst.

To use it, we define clover_mm256_epi16 such that it is set to 1 in each 16-bit chunk:

const __m256i dot_32 = _mm256_madd_epi16(clover_mm256_epi16, dot_16);
const __m256  dot_f  = _mm256_cvtepi32_ps(dot_32);

Finally, we perform the last multiplication in the block iteration with the corresponding scale, and accumulate it into the result. For that we can use an FMA instructions:

dot_product_acc = _mm256_fmadd_ps(scaled_rcp, dot_f, dot_product_acc);

Once all blocks are iterated, the last step is to horizontally add the values into the accumulator and return the result. A function that will get the job done is given with:

static inline float _mm256_haddf32_ps(__m256 acc)
{
    const __m128 left  = _mm256_extractf128_ps(acc, 1);
    const __m128 right = _mm256_castps256_ps128(acc);
    const __m128 x128  = _mm_add_ps(left, right);
    const __m128 x64   = _mm_add_ps(x128, _mm_movehl_ps(x128, x128));
    const __m128 x32   = _mm_add_ss(x64, _mm_shuffle_ps(x64, x64, 0x55));
    return  _mm_cvtss_f32(x32);
}

Clover Supported Routines

Appart from the dot routine each container implements the following routines:

The matrix container, namely CloverMatrix4, is represented similarly. The values and scales are stored as separate contiguous blocks of memory, both in row-major order. Sub-matrices of size 64 × 64 share the same scale. The length of each vector is padded to 128 elements, and the row and column size of the matrix is also padded to 128. Similar design decisions are made for CloverMatrix8. CloverMatrix16 and CloverMatrix32 do not contain scales. The following routines are available:

Each of these routines are implemented using SIMD code as much as possible. For each routine we provide scalar implementation having the same nomenclature, following _scalar for testing and validation purposes. When possible, we parallize the code using OpenMP and provide the same routines in threaded code folloging the _parallel suffix.

Performance Evaluation

We evaluated our implementation on an Intel Xeon CPU E3-1285L v3 3.10GHz Haswell with 32GB of RAM and 25.6 GB/s bandwidth to main memory, running Debian GNU/Linux 8 (jessie), kernel 3.16.43-2+deb8u3. We use the Intel ICC compiler 17.0.0, Intel IPP 2017.0.0 (r52494), and Intel MKL 2017.0.0 (Build 20160801). We use RDTSC to measure the cycle count for each test, performing 15 repetitions with warm cache, and using the median as a result. To avoid the effects of frequency scaling and resource sharing on the measurements, Turbo Boost and Hyper-Threading are disabled.

For each routine we derive a pseudo flop count, using the number of additions and multiplications required to perform the mathematical operations, and report our results in flops per cycle (F/C). The flop count for dot product and scale and add is 2 * n and for MVM it is 2 * n * n.

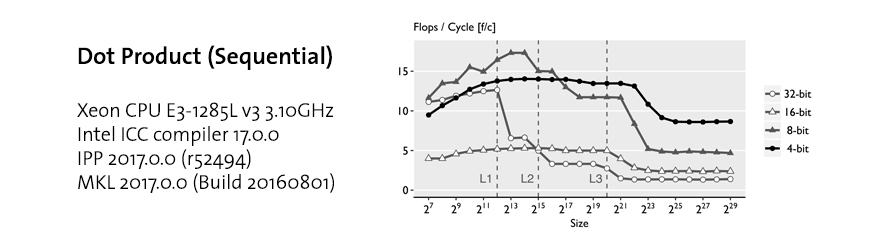
Dot Product. The figure below shows the performance profile of the dot product. When the data fits in L1 and L2 cache the 32-bit version is much faster than 4-bit because the entire computation is done using native instructions without bit-unpacking. Once the data exceed L3 cache, 4-bit is fastest since the dot product is memory bound: data movement from RAM becomes the bottleneck. The speed-up is up to 6x over the 32-bit version.

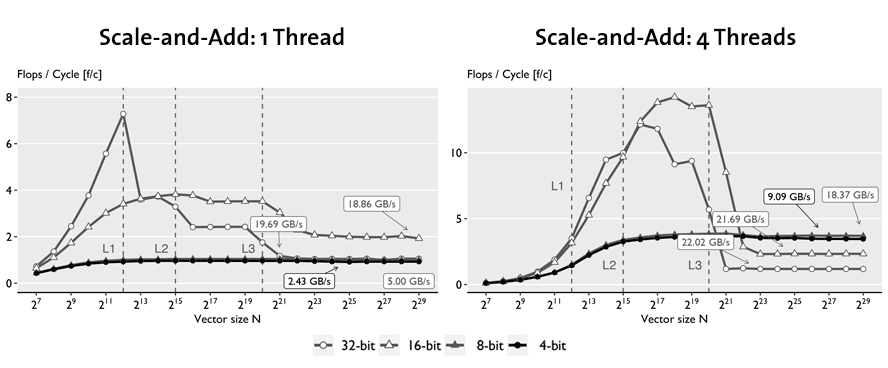
Scale and add. Similar to the dot product, the plots below shows that the 32-bit and 16-bit implementations are faster than 4-bit and 8-bit within cache for the same reasons. However, even outside L3 cache, 4- and 8-bit are only able to match the 32-bit implementation due to the higher overhead. This is reflected in the low bandwidth used. As a result, parallelization yields near-linear speed-up for 4-bit and near none for 32-bit, making 4-bit about 3x faster.

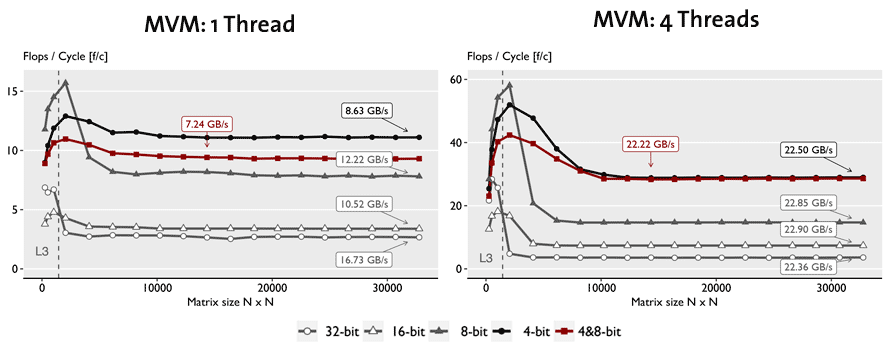
MVM. In the figure below we compare our sequential and parallel implementations of MVM, respectively, for each datatype, including the mixed 4,8-bit MVM. For the sequential case, for problems that do not fit in cache, we see that pure 4-bit is about 4.6x faster than 32-bit but uses only one third of the available bandwidth, and the mixed 4-bit and 8-bit MVM is noticeable slower. However, once parallelized, all version exhaust the available bandwidth and thus reach a speedup linear in the precision reduction. The mixed 4,8-bit MVM is now as fast as the 4-bit version since the bottleneck is loading the matrix.