HTHC: Heterogeneous Tasks on Homogeneous Cores
HTHC stands for Heterogeneous Tasks on Homogeneous Cores. It is a tool for fast training of generalized linear models (GLM) with a heterogeneous algorithm on a single instance of a multicore or manycore CPU.
Explanation
In the recent years, the CPUs have evolved from single core devices to machines composed of multiple cores. A notable example are standalone manycore processors with tens of cores running on a single socket, enabling them to catch up with the trend of high performance parallel programming which had been popularized by other manycore devices such as graphic cards.
One of commonly encountered use cases of this paradigm is machine learning. An instance of ML which we consider in our program are generalized linear models (GLM), widely used for fast regression and classification. The popular examples of GLMs are support vector machines and elastic networks.
Under the hood, GLMs are optimization tasks performed on the given datasets. Different approaches apply to these computations. A straightforward arrangement is to let the optimization iterate multiple times over the entire dataset. A more sophisticated approach picks the most relevant data points and processes them in a block fashion.
HTHC [1] applies the latter approach by running two tasks: one selects dynamically the most relevant data, while the other is running the optimizer. The declared target hardware is the second generation of Intel Xeon Phi processors (Knight Landing, Knights Mill) where we benefit from their fast scratchpad on-package memory by delegating to it the more compute-intensive optimizer task.
We gain a significant speedup against the straightforward implementation and from 2$\times$ to an order of magnitude against the state-of-the art when working with dense data. We also show that HTHC performs on par with DuHL [2] - an analoguous scheme implemented on a heterogeneous CPU-GPU system.
Details
Our algorithm uses Asynchronous Block Coordinate Descent with a duality-gap based coordinate selection scheme. The program consists of two tasks $\mathcal A$ and $\mathcal B$ running in parallel:
- Task $\bf{\mathcal A}$ performs coordinate selection based on the greatest contribution to the current global duality gap. If a separate high-bandwidth memory is available, it allocates its data to the regular memory.
- Task $\bf{\mathcal B}$ performs asynchronous updates on a block of coordinates selected by Task $\mathcal A$. The solver of choice is TPA-SCD [3]. If a separate high-bandwidth memory is available, it allocates its data to the high-bandwidth memory.
The scheme contains 4 levels of parallelism:
- Tasks A and B run in parallel to each other.
- Both tasks perform parallel updates on their own data: while A updates duality gaps of multiple coordinates at the same time, B executes updates over multiple data points in asynchronous fashion.
- Task B uses multiple threads per data point, parallelizing algebraic operations performed over the data vector: dot product and “axpy”.
- Both task use SIMD instructions (implemented with Intel Intrinsics for AVX-512) for their compute-heavy operations.
The number of threads given to each task can be controlled by hyperparameters given at the input: $T_\mathcal{A}$, $T_\mathcal{B}$ reflect the number of parallel updates and $V_\mathcal{B}$ reflects the number of threads per updated data point. Thus, the total number of threads used is $T_\mathcal{A}$ + $T_\mathcal{B} \cdot V_\mathcal{B}$.
The HTHC implementation considers two types of sparse GLM models: lasso (primal) and support vector machines (dual). We support three data representations: 32-bit dense, 32-bit sparse (represented by a format akin to compressed-sparse-column) and mixed 4/32-bit dense (where the 4-bit vectors are implemented using a modified version of the Clover Library [4]).
Note that our solver and coordinate selection scheme could be replaced with any algorithms which are able to operate on the input data coordinate-wise.
Experimental results
We compare our optimized HTHC (marked as “A+B” in the plots) implementation against different baselines:
- A naive, straightforward OMP implementation of HTHC, both atomic (“OMP”) and lock-free (“OMP-WILD”).
- An optimized implementation of the TPA-SCD single-task solver run over the entire dataset (“ST” using an optimal number of cores and “ST (A+B)” using the same number of cores as Task $\mathcal B$ in HTHC).
- State of the art CPU code: PASSCoDe [5] SVM and VowpalWabbit [6] lasso.
- DuHL: a CPU-GPU implementation of a similar scheme [2].
Comparison against OMP and single-task baselines
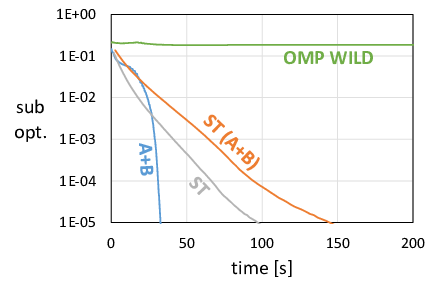
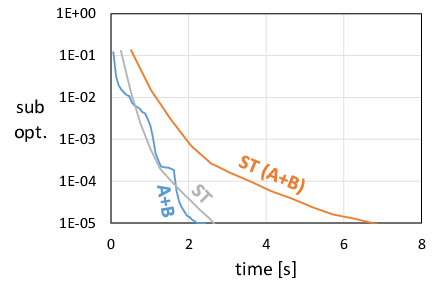
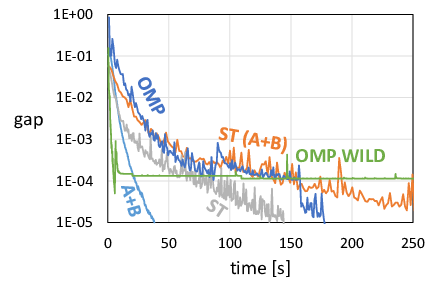
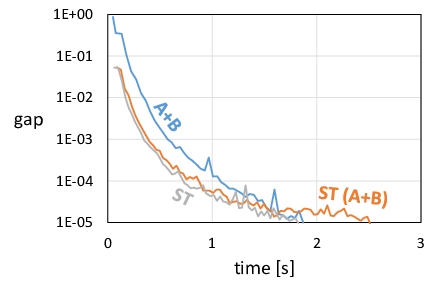
We present example plots obtained by running lasso and SVM on datasets of different density. For lasso, we plot suboptimality (the difference between the value current objective function and the value the optimization eventually converges to), and for SVM we plot the total duality gap as calculated by the Task $\mathcal A$.
The following plots show results for two datasets: the preprocessed Dogs vs. Cats dataset (dense), and the News20 dataset (sparse).
 |
 |
Lasso, Dogs vs. Cats |
Lasso, News20 |
 |
 |
SVM, Dogs vs. Cats |
SVM, News20 |
Comparison against state-of-the-art CPU code
We compare our SVM implementation against the atomic version of PASSCoDe and lasso against VowpalWabbit’s SGD. We measure time to reach the given classification accuracy and squared error respectively. We consider three datasets: the first two are dense, the last is sparse.
| Dataset | SVM Accuracy | A+B | ST | PASSCoDe-atomic | PASSCoDe-wild |
| Epsilon | 85% | 0.35 s | 1.11 s | 0.70 s | 0.64 s |
| Dogs vs. Cats | 95% | 0.51 s | 0.69 s | 2.69 s | 1.66 s |
| News20 | 99% | 0.14 s | 0.06 s | 0.02 s | 0.01 s |
| Dataset | Lasso Squared Error | A+B | ST | Vowpal Wabbit |
| Epsilon | 0.47 | 0.56 s | 0.62 s | 12.19 s |
| Dogs vs. Cats | 0.15 | 5.91 s | 23.37 s | 47.29 s |
| News20 | 0.32 | 0.94 s | 0.76 s | 0.02 s |
Comparison against CPU-GPU code
We compare our results against those presented in [2] for a CPU-GPU implementation of the scheme. We consider the Dogs vs. Cats dataset. We obtain 2$\times$ speedup for lasso and 2.5$\times$ speedup for SVM.
Source
The source code is available on GitHub. The target architecture is Intel Knights Landing, but various configuration variables are provided for compatibility with other Intel machines.
Main Reference
[1] Eliza Wszola, Celestine Mendler-Dünner, Martin Jaggi, Markus Püschel
On Linear Learning with Manycore Processors
CoRR abs/1905.00626 (2019)
Auxilliary References
[2] Celestine Dünner, Thomas P. Parnell, Martin Jaggi
Efficient Use of Limited-Memory Accelerators for Linear Learning on Heterogeneous Systems
Advances in Neural Information Processing Systems, pp. 4258–4267 (2017)
[3] Thomas Parnell, Celestine Dünner, Kubilay Atasu, Manolis Sifalakis, Haris Pozidis
Large-scale stochastic learning using GPUs.
IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), pp. 419–428 (2017)
[4] Alen Stojanov, Tyler Michael Smith, Dan Alistarh, Markus Püschel
Fast Quantized Arithmetic on x86: Trading Compute for Data Movement
IEEE International Workshop on Signal Processing Systems (SiPS), pp. 349–354 (2018)
[5] Cho-Jui Hsieh, Hsiang-Fu Yu, Inderjit S. Dhillon
PASSCoDe: Parallel ASynchronous Stochastic dual Co-ordinate Descent
International Conference on Machine Learning (ICML), pp. 2370–2379 (2015)
[6] John Langford, Lihong Li, Alex Strehl
VowpalWabbit
(online, retrieved 2019)

