Explanation

Numerical (subpolyhedra) domains are commonly used in static program analysis. Examples include box, pentagon, octagon, and polyhedra, each offering a different trade-off in accuracy and speed. In particular the most expensive polyhedra domain was long considered unpractical for applications as the join operator is exponential in the number of variables. We have developed a novel approach to and complete implementation of numerical domains (ELINA) that speeds up analysis by orders of magnitude, often without losing precision. We started with octagons [5] and polyhedra [4] and then generalized to all subpolyhedra domains [3]. In the cases where the method does not apply as is, we use learning to intelligently lose precision to make it applicable.

Key Ideas

Dynamic decomposition of polyhedra. During analysis, for many programs, not all variables develop relationships. This means that the polyhedra can be kept decomposed during analysis (corresponding to a partition of the variable set). However, the decomposition changes during analysis and has to be estimated before each operator is applied. The complexity of each operator is now determined by the largest block in the partition and not the number of variables, for join an exponential speedup. For example, the key theorem for the join [4] constructs a decomposition of the output from the inputs:

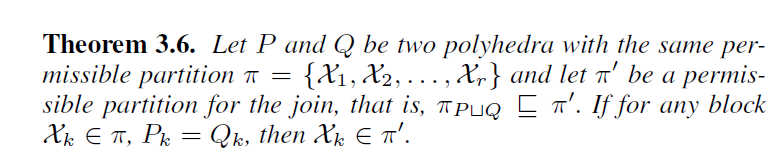
Decomposed polyhedra join

All subpolyhedra domains can be decomposed [3-5].

Reinforcement learning for losing precision. In the cases where the block sizes above become too large, we can enforce finer partitions by approximation a polyhedron by the direct product of its projections. How and when to do this requires a policy that we obtained automatically through reinforcement learning from a training set [2].

Experiments

The following table shows a sample of benchmarks for polyhedra analysis [3]. We compare our ELINA (the column “Our Decomposition” is a newer version of ELINA) against the prior PPL. Note that here ELINA does not lose precision compared to PPL. TO = timeout, MO = memoryout.

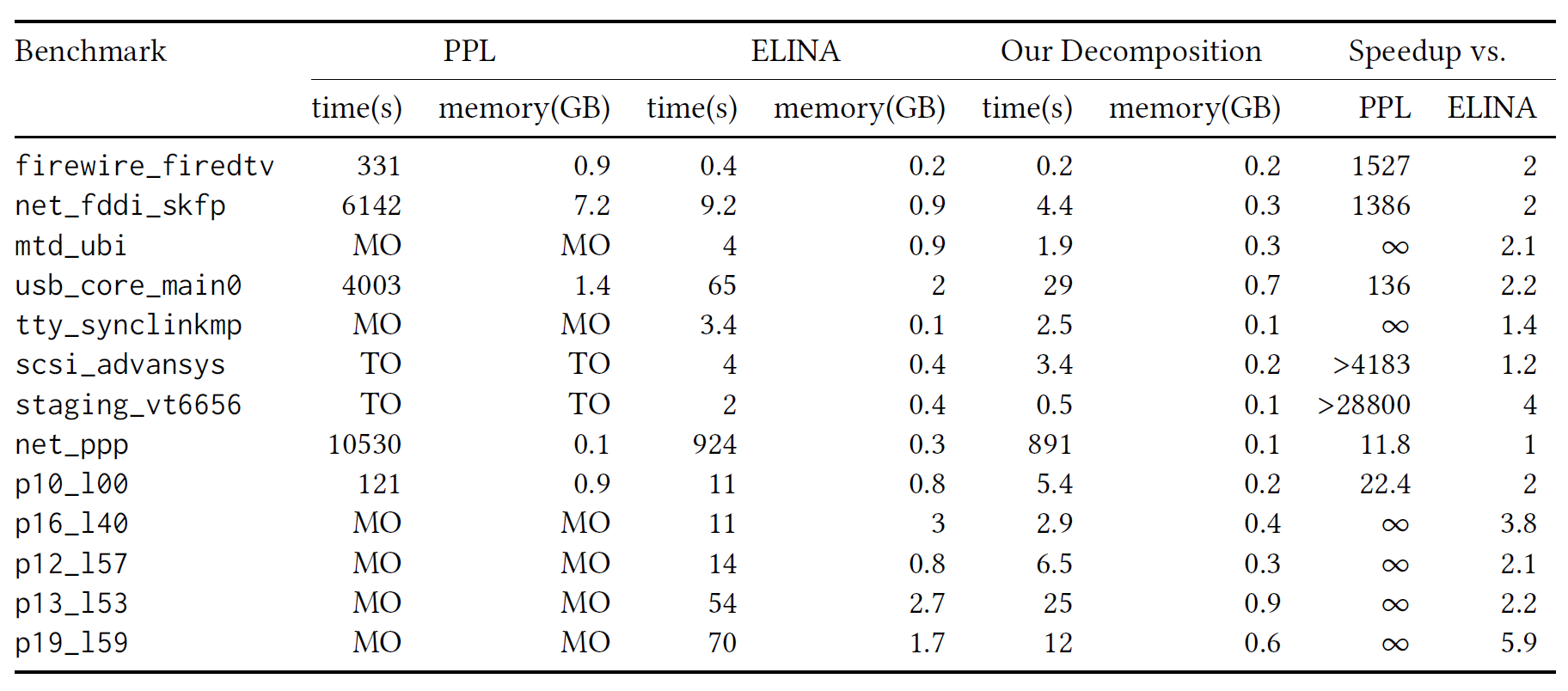
Speedups ELINA vs. PPL

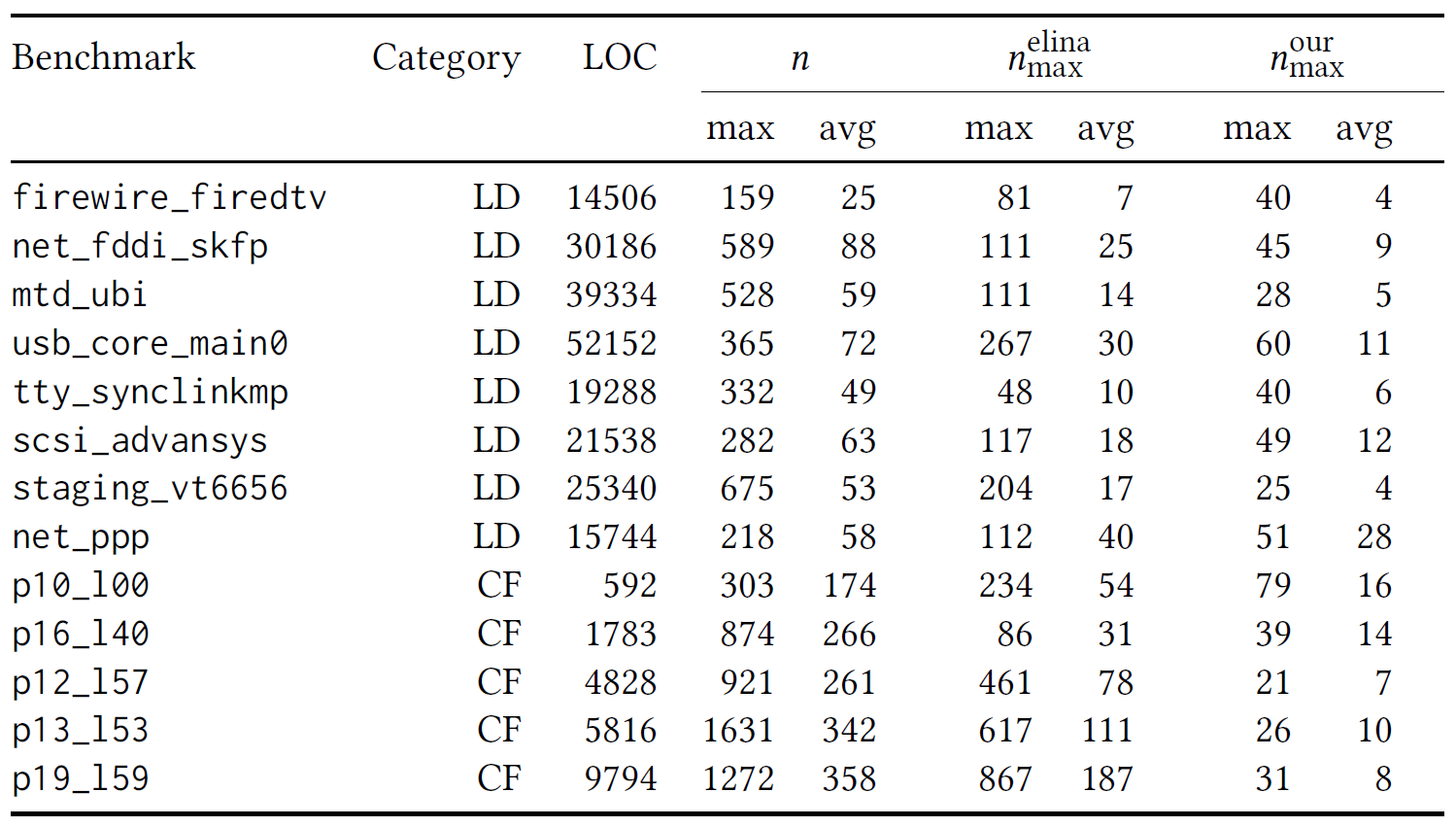
The reason for the speedups are the reduced block sizes shown in the following table.

Block sizes

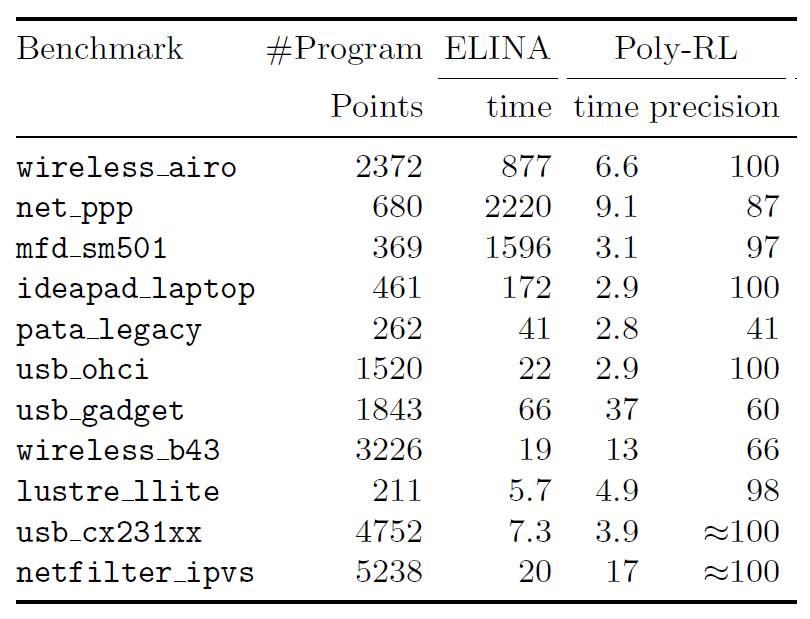
In cases where decomposition does not give a substantial speedup of several orders of magnitude, this speedup can still be achieved by approximation, using an RL-learned policy to optimize the speed/precision tradeoff [2].

Speedups RL-ELINA vs. ELINA

References

  1. ELINA website

  2. Gagandeep Singh, Markus Püschel, Martin Vechev Reinforcement Learning for Fast Program Analysis Proc. Computer-Aided Verification (CAV), pp. 211-229, 2018

  3. Gagandeep Singh, Markus Püschel, Martin Vechev A Practical Construction for Decomposing Numerical Abstract Domains Proc. Principles of Programming Languages (POPL), No. 55, 2018

  4. Gagandeep Singh, Markus Püschel, Martin Vechev Fast Polyhedra Abstract Domain Proc. Principles of Programming Languages (POPL), pp. 46-59, 2017

  5. Gagandeep Singh, Markus Püschel, Martin Vechev Making Numerical Program Analysis Fast Proc. Programming Languages Design and Implementation (PLDI), pp. 303-313, 2015